0. Intro
En los últimos tiempos, se está reavivando el debate público y en el mundo académico de los problemas que adolece la economía española. La mayor parte de académicos alcanzan una misma conclusión, la productividad española lleva practicamente dos décadas estancada. Recientemente la Fundación BBVA y el Ivie publicaron un informe en el que se muestra la comparativa de la evolución de la productividad española junto a otros países de la OCDE1. Resulta muy llamativo observar que para el periodo 2000-2022 la tasa de variación acumulada de la productividad total de los factores fue de un -7,3%, mientras que para países tales que, Alemania o Reino Unido la evolución fue muy diferente(11,8% y 8,8%, respectivamente).
Este problema como veremos a continuación, generará dificultades para mejorar el nivel de vida de la población española, además, limita la competitividad internacional debido a la menor eficiencia de nuestro sistema productivo.
En este trabajo analizaré las consecuencias a largo plazo que tendrá el estancamiento de la productividad española, además, propondré una mejora en el desarrollo del capital humano como medida para mejorar la productividad, basándome en las teorías de crecimiento éndogeno. Para ello los datos han sido extraídos del Banco de España y de las Penn World Tables a través del package pwt10.
1. Evolución del PIB per cápita para diversos países
En primer lugar, he realizado un gráfico donde se puede ver la serie histórica de la evolución del PIB per cápita para diferentes páises. Los datos de PIB están medidos en dólares de 2017 y ajustados por Paridad de Poder Adquisitivo (PPA).
Cabe destacar que se pueden observar dos grupos de países. Uno formado por páises de renta más alta (EEUU, Alemania, Francia) y otro con rentas más bajas (España, Portugal o Italia). En el presente trabajo trataremos de desentrañar que es lo que nos ha llevado a ser uno de estos países con un PIB per capíta relativamente más bajo y como podemos aumentarlo de cara al futuro.
Código
df_2 <- pwt10.01
df_3 <- df_2 %>%
filter(country %in% c("Spain", "France", "Germany", "Italy", "Portugal","United States of America", "Japan")) %>% select(country, year, pop, rgdpna, rgdpe, rgdpo,hc) %>%
mutate(pib_pc = rgdpo/pop,
pib_pc = round(pib_pc,2))
hc_2 <- df_3 %>% hchart('line', hcaes(x = 'year', y = 'pib_pc', group = 'country')) %>%
hc_title(text = "Evolución PIB per cápita,PPA($ de 2017)") %>%
hc_caption(text = "Fuente:Penn World Tables 10.01") %>%
hc_yAxis(title = "PIB per cápita") %>%
hc_xAxis(title = NULL)
hc_22. PIB español desagregado
En este punto, analizaremos la tasa de variación del PIB así como su descomposición.
En el gráfico siguiente observamos ciertos valores que destacan a simple vista. Por ejemplo, en el año 1961 tuvo lugar una tasa de crecimiento del PIB del 11,84%, causada mas que probalmente por la entrada en vigor del Plan de Estabilizacion en 1959. Otro dato a destacar es que en el año 2009 con la Gran Recesión se produjo la mayor caída del PIB de la serie estudiada(No he recogido datos hasta 2020).
Respecto a los componentes del PIB, es interesante ver como el consumo se comporta de manera procíclica, casi replicando los movimientos del PIB. Además del consumo, el otro componente que merece la pena resaltar es el gasto público, el cúal, practicamente solo se ha visto reducido tras el año 2012 y el rescate de Europa.
Código
ruta <- "./datos/datos_esp.xlsx"
df <- rio::import(ruta)
df <- df %>% rename(C = `Consumo privado`,
G = `Gasto Público`,
I = `Inversión`,
X = `Exportación de bienes y servicios`,
M = `Importación de bienes y servicios`)
df <- df %>% mutate(M = M*-1)
df <- df %>% pivot_longer(cols = 3:7, names_to = "componentes", values_to = "saldo")
df <- df %>% group_by(componentes) %>%
mutate(var_saldo_pib = ((saldo - lag(saldo))/lag(PIB))*100)
df <- df %>% mutate(variacion_pib = ((PIB - lag(PIB))/lag(PIB))*100)
g <- ggplot(data = df) +
geom_bar(data = df,aes(x = año, y = var_saldo_pib, fill = componentes),position = "stack", stat = "identity") +
geom_line(data = df, aes(año,variacion_pib), color = "red")
df <- df %>% mutate(var_saldo_pib = round(var_saldo_pib, 2),
variacion_pib = round(variacion_pib, 2))
hc <- df %>%
hchart(
'column', hcaes(x = 'año', y = 'var_saldo_pib', group = 'componentes'),
stacking = "normal") %>%
hc_add_series(df, "line", hcaes(año, variacion_pib), name = "PIB") %>%
hc_title(text = "Tasa de crecimiento del PIB y sus componentes") %>%
hc_xAxis(title = list(text = NULL)) %>%
hc_yAxis(title = list(text = "Porcentaje(%)")) %>%
hc_caption(text = "Fuente: Banco de España")
hc3. Descomponiendo el PIB per cápita
En esta sección he utilizado los datos de las Penn World Tables (PWT) para desagregar el PIB per cápita español y conocer mejor que hay detrás de este indicador. El PIB per capita puede descomponerse de la siguinete forma:
\[\ PIBpc = (PIB/empleo)*(empleo/población)\] Esta expresión nos muestra que el PIB per cápita esta compuesto por la productividad del trabajo (PIB/ empleo) y del empleo per cápita (empleo/población). En la tabla siguiente encontramos los resultados de la descomposición de la renta per cápita con datos desde el año 1951.
Código
df_product_1 <- df_2 %>% select(country, year, rgdpo, emp, pop) %>%
filter(country == "Spain") %>%
mutate(tc_pib = (rgdpo-lag(rgdpo))/lag(rgdpo),
tc_pop = (pop-lag(pop))/lag(pop),
tc_emp = (emp-lag(emp))/lag(emp)) %>%
mutate(tc_pib_pc = (tc_pib-tc_emp) + (tc_emp - tc_pop))
df_product_2 <- df_product_1 %>% mutate(tc_p_l = (tc_pib - tc_emp)*100,
tc_emp_pc = (tc_emp - tc_pop)*100,
tc_pib_pc = tc_pib_pc*100) %>%
select(country, year, tc_pib_pc, tc_p_l, tc_emp_pc) %>%
filter(!year == 1950) %>%
select(!country) %>%
mutate(`Contribución Productividad` = (tc_p_l/tc_pib_pc)*100,
`Contribución empleo per cápita` = (tc_emp_pc/tc_pib_pc)*100) %>%
rename(`PIB per cápita`= tc_pib_pc,
`Empleo per cápita` = tc_emp_pc,
`Productividad del trabajo` = tc_p_l,
Año = year) %>%
mutate(`PIB per cápita`= round(`PIB per cápita`,2),
`Empleo per cápita`= round(`Empleo per cápita`,2),
`Productividad del trabajo` = round(`Productividad del trabajo`,2),
`Contribución Productividad`= round(`Contribución Productividad`,2),
`Contribución empleo per cápita`= round(`Contribución empleo per cápita`,2)
)
## TABLA GT
tabla <- DT::datatable(df_product_2,
class = 'cell-border stripe',
caption = "Descomposición del PIB per cápita en tasas de variación",
colnames = c("Año", "PIB per cápita", "Productividad del trabajo", "Empleo per cápita", "Contribución Productividad(%)","Contribución empleo per cápita(%)")) %>%
formatStyle(c("Productividad del trabajo","Contribución Productividad" ),
backgroundColor = 'lightblue',
fontWeight = "bold") %>%
formatStyle(c("Empleo per cápita", "Contribución empleo per cápita"),
backgroundColor = "palegreen",
fontWeight = "bold") %>%
formatStyle("PIB per cápita",
backgroundColor = "aquamarine",
fontWeight = "bold")
tablaLas tasas de crecimiento de la productividad fueron bastante altas desde los 50 hasta las crisis del petróleo, momento en el que se empieza a ralentizar el avance. Durante los años 2000 el crecimiento es muy poco significativo, debido a que los mayores avances se dieron entre los años 2005-2007(años influenciados por la burbuja inmobiliraria). A partir de estos años se puede observar que sigue siendo positiva la tasa de crecimiento de la productivid, no obstante, esto se debe a un fenomeno estadístico. Hemos definido la productividad del trabajo como:\[ productividad = PIB/empleo\]
Por tanto el incremento de la productividad en estos años se debe tan solo a la masiva destrucción de empleo que sufrió la economía española como consecuencia de la crisis financiera de 2008. Para visualizar de manera más clara las variaciones en los componenetes del PIB per cápita he realizado la siguiente gráfica:
Código
df_plot <- df_product_2 %>% select(`Año`,`PIB per cápita` , `Productividad del trabajo`, `Empleo per cápita`)
df_plot <- df_plot %>% pivot_longer(cols = 3:4, names_to = "componentes_pibpc", values_to = "tasa_variacion")
df_plot <- df_plot %>% mutate(Componentes = componentes_pibpc)
plot <- ggplot() +
geom_bar(data = df_plot,aes(x = Año, y = tasa_variacion, fill = Componentes),position = "stack", stat = "identity") +
geom_line(data = df_plot, aes(Año, `PIB per cápita`), color = "darkblue") +
theme_economist_white() +
scale_x_continuous(breaks = seq(1955,2020,5)) +
labs(title = "Descomposición del PIB per cápita",
subtitle = "Tasas de variación en %",
guides = NULL,
x = NULL,
y = NULL,
caption = "Fuente: Penn World Tables 10.01",
color = "componentes")
plot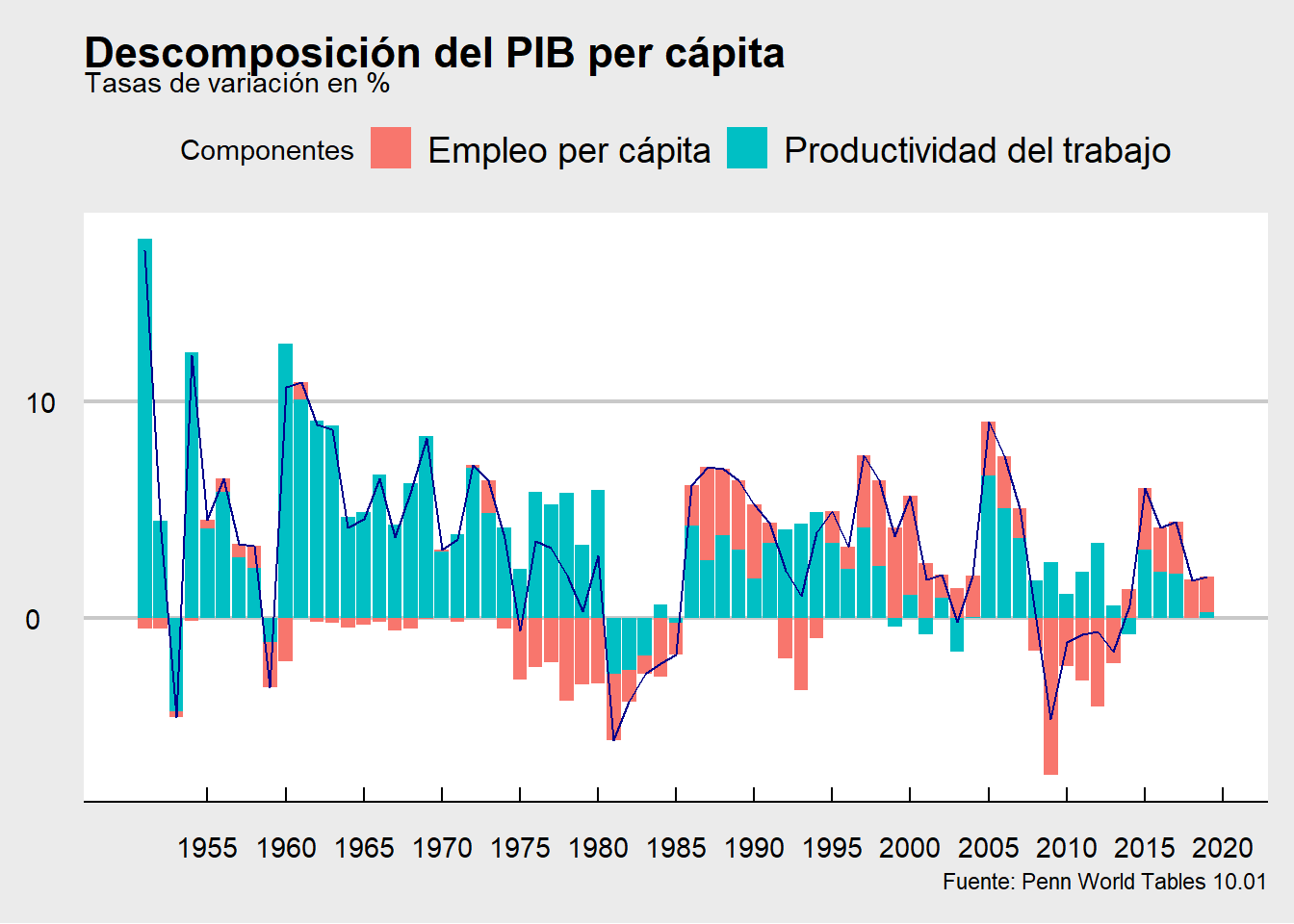
Este escenario nos lleva a una situación en la que la productividad del trabajo ha crecido de una manera poco significativa en los últimos 20 años. Uno de los factores que explican este resultado es el estancamiento de la productividad total de los factores(PTF). Como se puede observar a continuación, los incrementos de la productividad iban muy ligados a aumentos de la PTF. No obstante, en los años 2000 las mejoras en la PTF son muy reducidos generando problemas para conseguir mejoras en la productividad del trabajo. Por tanto nos encontramos con que la economía española lleva dos décadas perdidas en el avance de su productividad total de los factores.
Código
pl <- df_4 <- df_2 %>%
filter(country== "Spain") %>%
select(year,country,rtfpna) %>%
mutate(var_ptf = (rtfpna- lag(rtfpna))/lag(rtfpna),
var_ptf_per = var_ptf*100)
ptf <- ggplot()+
geom_col(data = pl, aes(year,var_ptf_per, fill = "PTF")) +
geom_line(data = df_product_2, aes( x = Año, y =`Productividad del trabajo`, color = "Productividad del trabajo")) +
scale_fill_manual(values = "#6B8E23", name = NULL) +
scale_color_manual(values = "#2F4F4F", name = NULL) +
theme_hc() +
labs(title = "Evolución de la productividad del trabajo y la PTF",
subtitle = "Tasa de variación en %",
caption = "Fuente: Penn World Tables 10.01",
y = NULL,
x = NULL,
fill = NULL,
color = NULL)
ptf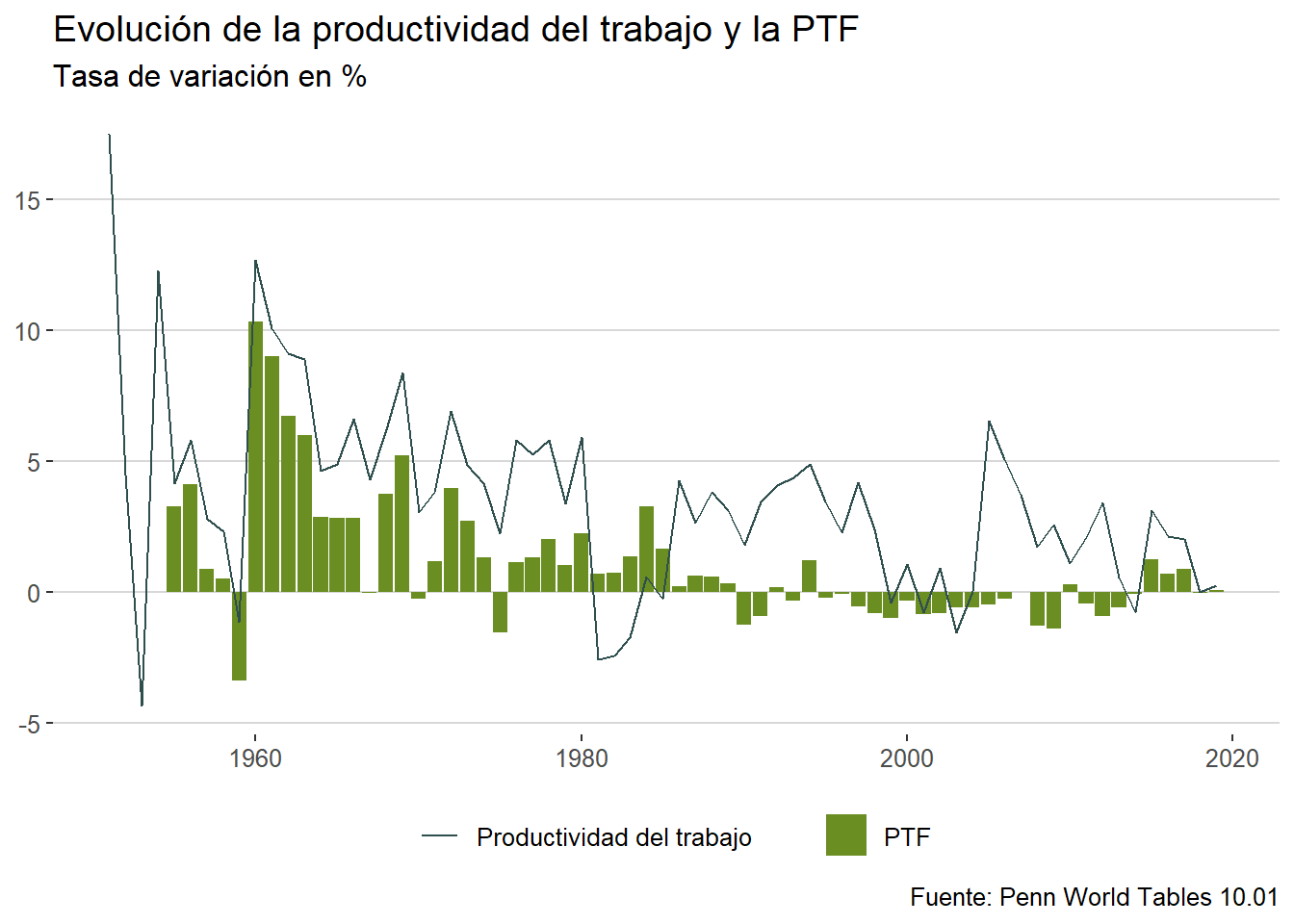
4. Importancia del capital humano
La PTF es comunmente llamada como “el residuo de Solow”. El residuo de Solow recibe este nombre en honor al gigante de la economía Robert Solow (recientemente fallecido a los 99 años, DEP Bob) cuyo famoso modelo hemos estudiado todos a lo largo de la carrera. El residuo basicamente viene a representar aquella proporción del output que no se puede explicar por las aportaciones de los factores productivos (Capital y Trabajo). Según el modelo de Solow, este residuo está determinado de forma exógena, es decir, viene dado, y por tanto el crecimiento de la renta per cápita de una economía a largo plazo que depende de dicho residuo también será exógeno. Este resultado es claramente insatisfactorio ya que según el modelo de Solow no se podria alterar la tasa de crecimiento del PIB per cápita a largo plazo a través de medidas de politíca económica.
Esta insatisfaccón llevo a los economistas a desarrollar una nueva clase de modelos. En los años 80 del siglo pasado aparecieron estos nuevos modelos conocidos como “modelos de crecimiento endógeno”. En este nuevo tipo de modelos los determinantes del crecimiento se determinan de manera endógena al modelo (al contrario de lo que ocurría en el modelo de Solow), y por tanto, sí que se puede ver afectada la tasa de crecimiento de la renta per cápita a largo plazo.
Entre los modelos de crecimiento endógeno más importantes destacan: El modelo de Lucas (desarrollado por el economista Robert Lucas, tambíen conocido por la famosa “Critica de Lucas” y sus aportaciones a las expectativas racionales), el cuál incluye en su función de producción el capital humano, asi como, el tiempo dedicado a acumular el mismo. Otro modelo a destacar es el de Romer, quién introduce la inversión en I+D como potenciador de la productividad y por tanto del crecimiento. Además existen muchos otros modelos de crecimiento endógeno desarrollados por importantes econmistas tales que: Barro, Rebelo o más recientemente, Acemoglu.
Lo apropiado en esta sección habría sido estimar alguno de estos modelos de crecimiento endógeno para observar si los datos respaldan dichas teorías, no obstante, dado el grado de complejidad requerido, he decidido realizar un análisis no tan riguroso pero que resalta la importancia de la educación en el crecimiento.
En primer lugar he estimado una función de producción Cobb Douglas que incluye el capital humano:
\[ Y = A \cdot K^\alpha \cdot (LH)^\beta \] Por tanto el modelo a estimar será: \[\ln(Y_t) = \beta_1 + \beta_2\ln(K) + \beta_3\ln(L) + \beta_4ln(H) + u_t\]
Código
| Observations | 3492 (9318 missing obs. deleted) |
| Dependent variable | log(gdp) |
| Type | OLS linear regression |
| F(3,3488) | 23704.04 |
| R² | 0.95 |
| Adj. R² | 0.95 |
| Est. | S.E. | t val. | p | |
|---|---|---|---|---|
| (Intercept) | 0.06 | 0.05 | 1.20 | 0.23 |
| log(k) | 0.56 | 0.01 | 77.31 | 0.00 |
| log(l) | 0.41 | 0.01 | 58.75 | 0.00 |
| log(hc) | 0.76 | 0.03 | 23.06 | 0.00 |
| Standard errors: OLS |
La estimación realizada recoge la muestra de todos los países que aparecen en las PWT. Como se puede observar, la variable del capital humano es estadisticamente significativa, no solo eso, si no que posee el coeficiente más grande. Por otra parte tambíen cabe destacar que el modelo se ajusta casi perfectamente con un R2 de 0.95.
Código
df_2019 <- df_2 %>% filter(year == 2019) %>%
mutate(pib_pc = rgdpo/pop) %>%
select(country,year,pib_pc, hc, pop) %>%
mutate(pib_pc = round(pib_pc, 2),
hc = round(hc, 2)) %>%
rename(`PIB per cápita` = pib_pc,
`Capital Humano` = hc,
`Población` = pop,
País = country)
gg <- ggplot(data = df_2019, aes(`PIB per cápita`, `Capital Humano`, size = `Población`, color = `Capital Humano`, label = País)) +
geom_point() +
geom_smooth(method = "lm") +
labs(title = "Capital Humano vs PIB per cápita,PPA($ de 2017)",
caption = "Fuente: Penn World Tables 10.01",
xlab = NULL,
ylab = NULL) +
scale_x_continuous(labels = scales::dollar_format()) +
theme_few()
ggplotly(gg)La relación entre capital humano y renta per cápita tambíen se puede observar en el gráfico anterior, donde se refleja el PIB per cápita en el año 2019, la población(en millones de personas) y el índice de capital humano. Claramente se observa la correlación positiva entre renta per cápita y capital humano. Aunque sabemos que correlación no tiene porque implicar causalidad, los modelos de crecimiento éndogeno mencionados anteriormente si que corroboran dicho efecto causal y por tanto, si queremos parecernos a otros países de Europa en cuanto a nivel de PIB per cápita se refiere, deberemos mejorar nuestros niveles de capital humano. Esta mejora del capital humano conseguirá incrementar la productividad del trabajo y por tanto la renta de la población española en el largo plazo.
Conclusión
Finalmente, me gustaría resaltar que el estancamiento de la productividad española es problemático, debido a que, sin mejoras en la productividad no conseguiremos hacer crecer nuestra renta en el largo plazo, y por tanto, tampoco lo hará el nivel de vida de nuestros ciudadanos.
En este trabajo he intentado resaltar la importancia del capital humano debido a su capacidad de generar mayores niveles de productividad, así como, su relevancia como factor de producción a tener en cuenta junto al capital físico y al trabajo.
Dicha mejora del capital humano debe venir de la mano de la mejora en el proceso de acumulación de capital humano, el cuál, está estrechamente relacionado con el sistema educativo. La mejora de la educación formal no tiene que venir solo de posibles aumentos del gasto en educación, sino que, se debe hacer enfasis en los métodos de aprendizaje o en los propios contenidos impartidos. Actualmente nos encontramos con planes de estudio en universidades totalmente desfasados y paralelos al mundo profesional, donde se enseñan conocimientos y habiliadades que no se demandan en el mercado laboral(Menos mal que llegó Pedro para enseñarnos R…😉).
Por último (ahora de verdad), considero que más asiganturas como esta deberían ser añadidas en el plan de Economía, ya no solo porque muchas de las asignaturas que nos imparten son prácticamente una pérdida de tiempo, sino porque asignaturas como programación te ayudan a desarrollar una skill básica en el mundo de la Economía, la cuál es altamente demandada, bien quieras dedicarte al mundo profesional o al mundo de la investigación.
Información sobre la sesión
Abajo muestro mi entorno de trabajo y paquetes utilizados
current session info
─ Session info ───────────────────────────────────────────────────────────────
setting value
version R version 4.3.1 (2023-06-16 ucrt)
os Windows 10 x64 (build 19045)
system x86_64, mingw32
ui RTerm
language (EN)
collate Spanish_Spain.utf8
ctype Spanish_Spain.utf8
tz Europe/Madrid
date 2024-01-22
pandoc 3.1.1 @ C:/Program Files/RStudio/resources/app/bin/quarto/bin/tools/ (via rmarkdown)
─ Packages ───────────────────────────────────────────────────────────────────
package * version date (UTC) lib source
assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.3.1)
backports 1.4.1 2021-12-13 [1] CRAN (R 4.3.0)
broom 1.0.5 2023-06-09 [1] CRAN (R 4.3.1)
bslib 0.6.1 2023-11-28 [1] CRAN (R 4.3.2)
cachem 1.0.8 2023-05-01 [1] CRAN (R 4.3.1)
cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.3.1)
cli 3.6.1 2023-03-23 [1] CRAN (R 4.3.1)
clipr 0.8.0 2022-02-22 [1] CRAN (R 4.3.1)
colorspace 2.1-0 2023-01-23 [1] CRAN (R 4.3.1)
crayon 1.5.2 2022-09-29 [1] CRAN (R 4.3.1)
crosstalk 1.2.0 2021-11-04 [1] CRAN (R 4.3.1)
curl 5.0.2 2023-08-14 [1] CRAN (R 4.3.1)
data.table 1.14.8 2023-02-17 [1] CRAN (R 4.3.1)
desc 1.4.2 2022-09-08 [1] CRAN (R 4.3.1)
details 0.3.0 2022-03-27 [1] CRAN (R 4.3.2)
digest 0.6.33 2023-07-07 [1] CRAN (R 4.3.1)
dplyr * 1.1.3 2023-09-03 [1] CRAN (R 4.3.1)
DT * 0.29 2023-08-29 [1] CRAN (R 4.3.1)
ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.3.1)
evaluate 0.23 2023-11-01 [1] CRAN (R 4.3.2)
fansi 1.0.5 2023-10-08 [1] CRAN (R 4.3.2)
farver 2.1.1 2022-07-06 [1] CRAN (R 4.3.1)
fastmap 1.1.1 2023-02-24 [1] CRAN (R 4.3.1)
fontawesome 0.5.2 2023-08-19 [1] CRAN (R 4.3.1)
forcats * 1.0.0 2023-01-29 [1] CRAN (R 4.3.1)
generics 0.1.3 2022-07-05 [1] CRAN (R 4.3.1)
ggplot2 * 3.4.4 2023-10-12 [1] CRAN (R 4.3.2)
ggthemes * 4.2.4 2021-01-20 [1] CRAN (R 4.3.1)
glue 1.6.2 2022-02-24 [1] CRAN (R 4.3.1)
gt * 0.9.0 2023-03-31 [1] CRAN (R 4.3.1)
gtable 0.3.4 2023-08-21 [1] CRAN (R 4.3.1)
gtExtras * 0.5.0 2023-09-15 [1] CRAN (R 4.3.2)
highcharter * 0.9.4 2022-01-03 [1] CRAN (R 4.3.2)
hms 1.1.3 2023-03-21 [1] CRAN (R 4.3.1)
htmltools 0.5.7 2023-11-03 [1] CRAN (R 4.3.2)
htmlwidgets 1.6.4 2023-12-06 [1] CRAN (R 4.3.2)
httr 1.4.7 2023-08-15 [1] CRAN (R 4.3.1)
igraph 1.5.1 2023-08-10 [1] CRAN (R 4.3.2)
jquerylib 0.1.4 2021-04-26 [1] CRAN (R 4.3.1)
jsonlite 1.8.8 2023-12-04 [1] CRAN (R 4.3.2)
jtools * 2.2.2 2023-07-11 [1] CRAN (R 4.3.2)
kableExtra 1.3.4 2021-02-20 [1] CRAN (R 4.3.1)
knitr 1.45 2023-10-30 [1] CRAN (R 4.3.2)
labeling 0.4.3 2023-08-29 [1] CRAN (R 4.3.1)
lattice 0.21-8 2023-04-05 [2] CRAN (R 4.3.1)
lazyeval 0.2.2 2019-03-15 [1] CRAN (R 4.3.1)
lifecycle 1.0.4 2023-11-07 [1] CRAN (R 4.3.2)
lubridate * 1.9.2 2023-02-10 [1] CRAN (R 4.3.1)
magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.3.1)
Matrix 1.6-1.1 2023-09-18 [1] CRAN (R 4.3.1)
mgcv 1.8-42 2023-03-02 [2] CRAN (R 4.3.1)
munsell 0.5.0 2018-06-12 [1] CRAN (R 4.3.1)
nlme 3.1-162 2023-01-31 [2] CRAN (R 4.3.1)
paletteer 1.5.0 2022-10-19 [1] CRAN (R 4.3.2)
pander 0.6.5 2022-03-18 [1] CRAN (R 4.3.1)
pillar 1.9.0 2023-03-22 [1] CRAN (R 4.3.1)
pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.3.1)
plotly * 4.10.2 2023-06-03 [1] CRAN (R 4.3.1)
png 0.1-8 2022-11-29 [1] CRAN (R 4.3.1)
purrr * 1.0.2 2023-08-10 [1] CRAN (R 4.3.1)
pwt10 * 10.01-0 2023-02-27 [1] CRAN (R 4.3.1)
quantmod 0.4.25 2023-08-22 [1] CRAN (R 4.3.1)
R.methodsS3 1.8.2 2022-06-13 [1] CRAN (R 4.3.0)
R.oo 1.25.0 2022-06-12 [1] CRAN (R 4.3.0)
R.utils 2.12.2 2022-11-11 [1] CRAN (R 4.3.1)
R6 2.5.1 2021-08-19 [1] CRAN (R 4.3.1)
RColorBrewer * 1.1-3 2022-04-03 [1] CRAN (R 4.3.0)
Rcpp 1.0.11 2023-07-06 [1] CRAN (R 4.3.1)
readr * 2.1.4 2023-02-10 [1] CRAN (R 4.3.1)
readxl 1.4.3 2023-07-06 [1] CRAN (R 4.3.1)
rematch2 2.1.2 2020-05-01 [1] CRAN (R 4.3.1)
rio * 1.0.1 2023-09-19 [1] CRAN (R 4.3.1)
rlang 1.1.1 2023-04-28 [1] CRAN (R 4.3.1)
rlist 0.4.6.2 2021-09-03 [1] CRAN (R 4.3.2)
rmarkdown 2.25 2023-09-18 [1] CRAN (R 4.3.1)
rprojroot 2.0.3 2022-04-02 [1] CRAN (R 4.3.1)
rstudioapi 0.15.0 2023-07-07 [1] CRAN (R 4.3.1)
rvest 1.0.3 2022-08-19 [1] CRAN (R 4.3.1)
sass 0.4.8 2023-12-06 [1] CRAN (R 4.3.2)
scales 1.2.1 2022-08-20 [1] CRAN (R 4.3.1)
sessioninfo 1.2.2 2021-12-06 [1] CRAN (R 4.3.2)
stargazer * 5.2.3 2022-03-04 [1] CRAN (R 4.3.1)
stringi 1.7.12 2023-01-11 [1] CRAN (R 4.3.0)
stringr * 1.5.1 2023-11-14 [1] CRAN (R 4.3.2)
svglite 2.1.1 2023-01-10 [1] CRAN (R 4.3.1)
systemfonts 1.0.4 2022-02-11 [1] CRAN (R 4.3.1)
tibble * 3.2.1 2023-03-20 [1] CRAN (R 4.3.1)
tidyr * 1.3.0 2023-01-24 [1] CRAN (R 4.3.1)
tidyselect 1.2.0 2022-10-10 [1] CRAN (R 4.3.1)
tidyverse * 2.0.0 2023-02-22 [1] CRAN (R 4.3.1)
timechange 0.2.0 2023-01-11 [1] CRAN (R 4.3.1)
TTR 0.24.3 2021-12-12 [1] CRAN (R 4.3.1)
tzdb 0.4.0 2023-05-12 [1] CRAN (R 4.3.1)
utf8 1.2.4 2023-10-22 [1] CRAN (R 4.3.2)
vctrs 0.6.3 2023-06-14 [1] CRAN (R 4.3.1)
viridisLite 0.4.2 2023-05-02 [1] CRAN (R 4.3.1)
webshot 0.5.5 2023-06-26 [1] CRAN (R 4.3.1)
withr 2.5.2 2023-10-30 [1] CRAN (R 4.3.2)
xfun 0.41 2023-11-01 [1] CRAN (R 4.3.2)
xml2 1.3.5 2023-07-06 [1] CRAN (R 4.3.1)
xts 0.13.1 2023-04-16 [1] CRAN (R 4.3.1)
yaml 2.3.8 2023-12-11 [1] CRAN (R 4.3.2)
zoo 1.8-12 2023-04-13 [1] CRAN (R 4.3.2)
[1] C:/Users/Lenovo/AppData/Local/R/win-library/4.3
[2] C:/Program Files/R/R-4.3.1/library
──────────────────────────────────────────────────────────────────────────────